Af Rasmus Dalsgaard
Hvor mange penge skal du sætte på et spil: hvad er den korrekte indsats for DIG? Svaret får du - sort på hvidt og dokumenteret - i denne artikel om Money Management og indsats-udregning, skrevet af matematikkyndige Rasmus Dalsgaard (der i BetXperts forum kendes under navnet allan_urban)...
Et spilobjekt og kapital er i princippet det eneste, der skal til for at kaste sig ud i gamblingens dragende verden. Har vi noget at spille på, og noget at spille med, ja så vil der altid være potentiale for at lave profit.
Spilobjekter løber vi aldrig tør for. Det skal de mange bookmakere nok sørge for, men hvad med kapitalen? Den er ikke givet, og den vi har, skal vi sørge for at passe på. Hvis først hele kapitalen er tabt, har vi mistet evnen til at spille.
I forlængelse heraf er derfor vigtigt at administrere kapitalen så godt som man kan. Fra pokeren kender de fleste måske udtrykket a chip and a chair. Så længe man har chips ved pokerbordet, er man med, og har chancen for at vinde. Når man mister sin sidste chip, er man ude og har mistet muligheden for at vinde.
Den situation skal man for alt i verden undgå at havne i; det er ekstremt vigtigt at passe på den kapital man har. Hele denne øvelse kalder vi for money management.
Risiko vejer tungere end værdi
Money management går i alt sin enkelthed ud på at tilpasse indsatsstørrelsen på et givent spil efter den kapital man har til rådighed, samt spillets risiko og værdi.
Mange tror, at indsatsens størrelse kun skal afgøres af spillets værdi. Dette er imidlertid ikke korrekt. Et spil med lav værdi og lav risiko vil, ud fra en money management-betragtning, oftest kunne bære en større indsats end et med høj værdi og høj risiko.
Vigtigheden af at passe på sin kapital kan ikke understreges nok, og derfor er det en meget vigtig del af betting, at man sætter et indskud af den rigtige størrelse. Det må ikke blive for stort, da vi i tilfælde af tab ville gøre et for stort indhug i kapitalen. Omvendt må det heller ikke blive for lille, da vi i så fald ikke vinder nok i tilfælde af gevinst.
Denne artikel vil kaste et lys over hvilke faktorer der bør indgå, når man bestemmer indskudsstørrelsen på sine spil.
Se betting som investering – og hold fingrene fra formuen
Hvis man virkelig vil optimere sin indtjening, så bør man se på betting som en investering, på lige fod med investering i eksempelvis aktier og ejendomme. Det behøver slet ikke at være så kompliceret, og ved at gøre nogle få ting rigtigt, så kan man over tid øge profitten ganske betragteligt.
Afsæt en sum til betting. Og hold så fingrene fra den. Formuer har det på mange måder som træer. Hvis de får den rette pleje og de rigtige betingelser, så kan de vokse sig rigtigt store. Det nytter bare ikke noget hvis man skærer træet ned, hver gang den når til en vis højde – så får det aldrig mulighed for at vokse sig rigtigt stort.
Herunder ses forskellen på hvordan to formuer udvikler sig over 20 år. Begge vokser med 10% årligt, men den ene trækker 50% af overskuddet ud og geninvesterer kun halvdelen.
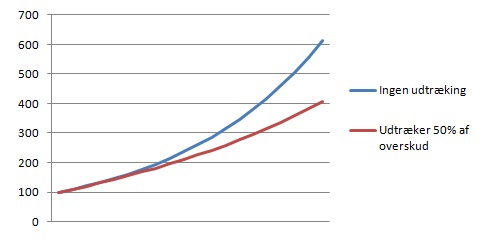
Hvis man endelig vil trække eventuel profit ud, så gør det sjældent og ikke mere end én gang, maksimalt to gange, om året.
Risiko kontra afkast
Afkast og risiko hænger sammen som ærtehalm. Som investor stræber man altid efter at øge sit afkast og reducere sin risiko. Hvis man skal vælge imellem at placere sine penge i to forskellige aktier, så vil man altid vælge den, der giver det højeste forventede afkast af de to, hvis risikoen er den samme. Omvendt så vil man altid vælge den aktie med den laveste risiko, hvis det forventede afkast er det samme.
Investoren bryder sig ikke om usikkerhed og volatilitet. Det vil være meget rarere at lave et fast afkast på 10% hvert år, end på skift tabe 10% og vinde 22%, selvom det i det lange løb giver det samme afkast. Indenfor betting er problemstillingen den samme.
Når vi analyserer et spil, så kommer vi frem til både en chancevurdering og en bet value (forholdet mellem chancevurderingen og oddset). Bet valuen er det forventede afkast på spillet, mens chancevurderingen kan ses som et udtryk for risikoen. Jo højere chancevurdering, jo mindre risiko - og omvendt. Normalt vil mange udtrykke risiko i varians eller volatilitet, men det er helt legalt at anse chancevurderingen som et udtryk for risiko. Antag følgende eksempel:
-
Spil 1: cv på 75%, odds 1,40
-
Spil 2: cv på 25%, odds 4,20
Fælles for de to spil er, at bet valuen er præcis 105%. Hvis vi spillede uendeligt mange spil, ville vi altså forvente præcis det samme afkast på de to spil, nemlig 5 units i overskud for hver 100 units omsat.
Variansens på de to spil er dog vidt forskellig. Variansen for spil 2 er i dette eksempel ni gange større end for spil 1. Det betyder langt større udsving, som det ses af nedenstående graf, der er simuleret over 1000 spil og med én unit per spil for både spil 1 og 2. Overskud er noteret på Y-aksen, mens antal spil er på X-aksen.
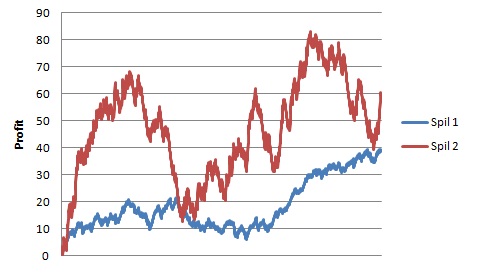
Selvom det forventede afkast af de to spil er præcis den samme, så er det tydeligt at se hvor stor forskel, der er på de enkelte grafer. Ved lav-odds spillet får vi et mere stabilt afkast uden de helt store udsving. Det betyder at vi kan risikere en større del af formuen, idet vi ved at risikoen for at mange tabte spil i træk er lille.
Omvendt, så kan vi ved det mere risikable høj-odds spil kun kan tillade en mindre del af formuen, idet den vil være udsat for langt større udsving. Det er selvfølgelig rart i de tider hvor det går godt, men vi skal ikke ind i en særligt dårlig stime, før vi har sat det hele til.
Hvis vi i stedet justerer indskuddet, vil vi få et langt mere stabilt afkast. I nedenstående graf er udgangspunktet det samme som før. Eneste ændring er, at der kun er spillet 1/3 unit på spil 2, mens spil 1 stadig får én unit.
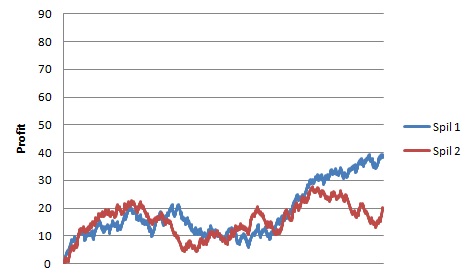
På spil med større risiko kan man ved at gøre et mindre indskud reducere variansen.
Det optimale indskud: Kelly-formlen
Enhver investor bør altid tilstræbe at optimere sin portefølje, således at den giver det bedste afkast i forhold til den givne risiko. Det gælder naturligvis også for betting. Her har vi selv indflydelse på indskuddet, og ved at sætte det rigtige indskud, er det muligt at optimere profitten.
Tilbage i 1956 præsenterede J.L. Kelly Jr. en formel brugt til at udregne den optimale indsats på et væddemål med en given chancevurdering og et givent odds. Dette kaldes for Kelly-strategien. I det lange løb vil denne strategi gøre det bedre end nogen anden strategi.
Kelly-formlen ser, lettere omskrevet, ud som følger:
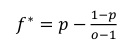
Hvor f* er andelen af kapitalen der skal placeres på spillet;
p er sandsynligheden for at spillet går hjem;
o er det decimalodds spillet giver.
Hvis vi tager udgangspunkt i spil 1 og spil 2 fra tidligere, skulle de to bet ifølge Kelly-strategien altså have:
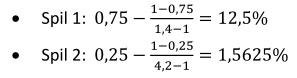
Lad os introducere spil 3 med følgende parametre: CV = 0,25; Odds = 5 (Bet value = 125%)
Kelly-bettet bliver således:
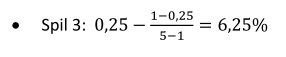
Det er ganske interessant at se på hvor stort et indskud, hvert af de tre spil skal have ifølge Kelly-strategien. Spil 3 skal have et større indskud end spil 2. Det siger næsten sig selv. Risikoen ved de to spil er ens, men det forventede afkast er større ved spil 3.
Ligeledes ser vi at spil 1 skal have et større indskud end spil 3. Det forventede afkast er væsentligt lavere, men ligeledes er risikoen meget mindre. Heraf kan vi generelt sige:
Risikoen ved spillet er vigtigere for indsatsen end værdien er, men samtidigt skal der tages højde for værdi, således at større værdi bør have et større indskud.
Kelly-metode er bedst, men kun på papiret
Kelly viste at metoden var en optimal strategi. Der er således ikke andre indsatsstrategier, der giver et større afkast over tid. At følge strategien slavisk er dog næppe nogen god idé, for der er en række problemstillinger, som gør at en mere konservativ tilgang er at foretrække. Selv tilhængere af Kelly argumenterer ofte for at man kun bør spille en del af det, som Kelly-strategien foreslår.
For det første, så er det en forudsætning for Kelly-metoden, at man har et tilpas stort antal af hvert spil. Det kan man naturligvis ikke få, for hver kamp spilles kun en enkelt gang. Vi kunne i stedet argumentere for at så længe man kunne finde spil nok med nogenlunde samme parametre (CV og BV), så var det fint nok.
På BetXpert blev der i år 2010 eksempelvis udlagt 2882 analyser med en gennemsnitlig bet value på knap 108. Det ville også være nok til at opfylde kravet til mange spil. Den dag man falder over et spil med en CV på 75% og odds 2, så skal man imidlertid op og sætte 50% af kapitalen. Den slags spil kommer der ikke nok af til at udligne variansen. Desuden er der en reel risiko for, at man har lavet en klar fejlvurdering, nå man er så uenig med bookmakeren.
Chancevurdering: Vær forsigtig
Det bringer os straks videre til næste problemstilling: chancevurderingen. For at beregne Kelly-indsatsen har vi brug for en chancevurdering af spillet. Denne vurdering vil altid være et skøn, for der findes ingen facitliste. Hvis man følger Kelly-strategien bliver man straffet hårdere ved at være for optimistisk, end ved at være for konservativ. Blot få procenter for meget på et udfald, har stor betydning for hvor stort et indskud man skal gøre.
Ved at tage en større risiko (højere indskud) øges sandsynligheden for både meget gode (høj vækst i kapitalen) og meget dårlige (stort indhug i kapitalen) resultater. En vigtig egenskab ved Kelly, er at man ved at gøre et for stort indskud nedsætter sandsynligheden for et meget godt resultat, mens man stadig øger sandsynligheden for et meget dårligt resultat. Derfor giver det god mening at være mere konservativ end hvad Kelly-strategien.
Undgå ondt i maven
Det er muligt at man i sidste ende får det bedste resultat ved at følge Kelly-strategien. Men hvad med tiden fra nu og indtil man gør det hele op. Det er fint nok at vi om ti år har 100-doblet kapitalen, men hvordan ville man have det hvis man om seks måneder havde sat halvdelen til?
Kelly-strategien er og bliver en meget fluktuerende strategi, hvor det går meget op og meget ned, og det kræver en enorm stærk psyke at sige til sig selv at det med tiden er den rigtige løsning, hvis man lige har tabt halvdelen af sin formue på 5 spil. En mere konservativ tilgang giver færre udsving.
I forlængelse heraf skal det sidste argument være netop psyken. Det psykologiske element er en vigtig faktor. Nogle folk har mere nytte af at placere en mindre indsats, end det som Kelly-strategien siger. Det nytter ikke noget at man ligger søvnløs eller udvikler kronisk tynd mave, fordi man jævnligt har 10% af sin samlede kapital på højkant på et enkelt spil.
Bedre end den "optimale" metode?
Vi har lige set, hvorfor der er flere gode grunde til ikke at benytte den optimale strategi. Men hvad skal man så gøre? Herunder vil vi se på tre alternative metoder og teste dem imod hinanden.
Metode 1: Flatbetting
Ren flatbetting har den fordel at det er nemt. Men meget mere kan tilhængere heller ikke vride ud af den. Flatbetting i dens simpleste forstand, hvor man uanset risiko, værdi eller kapital sætter et fast beløb på hvert spil, har den egenskab, at man i nedgangstider taber en større og større andel af sin kapital, mens man i opgangstider vinder mindre og mindre.
Begge dele må betegnes som særdeles utiltalende. Væksten i en kapital, hvor man benytter et fast beløb som indsats er, hvis vi ser bort fra varians, lineær.
Metode 2: Flatbetting v2.0
I stedet for at benytte et fast beløb, var en anden mulighed at benytte en fast procentdel af kapitalen som indskud. Kapitalen vil både i med- og modgang foretrække denne løsning frem for spil med et fast beløb. Væksten i kapitalen er her eksponentiel.
Dette kan nemt illustreres med et syn på de to ekstremer. Det ene yderpunkt er hvor man vinder 100 spil i træk (odds 2). Dette er de to øverste grafer i nedenstående diagram. Det modsatte yderpunkt er hvor man taber 100 spil i træk, hvilket vises i de to nederste grafer.
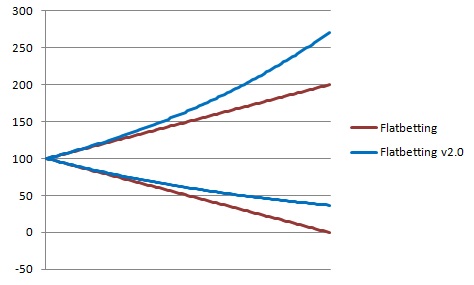
I begge tilfælde er metoden med en fast procentdel den overlegne. Bemærk også at man, ved at spille et fast beløb uden at justere sin indsats rammer 0 efter 100 tabte spil i træk. Det kan i teorien aldrig ske hvis man benytter en procentdel, da kapitalen vil aftage eksponentielt. At spille en procentdel frem for et fast beløb betyder reelt at man justerer sit indskud efter hvert eneste spil. Sagt på en anden måde:
Justér indskuddet så ofte som muligt, helst efter hvert spil, det betaler sig i det lange løb.
Metode 3: Det rigtige indskud?
Lad os slutteligt se på en metode til at beregne sit indskud, hvor vi tager højde for risiko og værdi, men vægter risiko højere, og hvor vi samtidigt automatisk justerer vores indskud efter hvert spil:
![]()
Hvor f* er andelen af kapitalen der skal placeres på spillet;
p er sandsynligheden for at spillet går hjem (chancevurdering);
r er en risikofaktor med en værdi imellem 0 og 1 (ex: 0,02 betyder 2% af kapitalen)
b er bet valuen på spillet.
Eksempel:
CV: p=50% > spilbar ned til 2,00 = o0
odds = 2,12
BV = 1,06
r = 0,03
f* = 0,5*0,03*1,06 = 1,59%
Da vi ved at chancevurdering og det fair odds er hinandens reciprokke værdi (p = o0-1), kan formlen også skrives som:
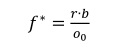
Hvor o0 er det fair odds, altså det odds som spillet er spilbart ned til.
Eksempel:
f* = r*b/o0
f*=0,03*1,06/2 = 1,59%
De tre spil der tidligere blev introduceret, vil derfor, med en risikofaktor på 0,02, skulle have følgende indskud:
-
Spil 1: 0,75 x 0,02 x 105 = 1,575% (Kelly-metode = 12,5%)
-
Spil 2: 0,525% (Kelly-metode = 1,5625%)
-
Spil 3: 0,625% (Kelly-metode = 6,25%)
Her tages der både højde for hvor risikabelt spillet er, i form af spillets CV, men samtidig får højere værdi et højere indskud. Risikofaktoren bestemmer hvor meget man maksimalt kan tabe på et spil. Væksten i kapitalen er her eksponentiel.
Bemærk: Hvis man finder et spil med tilstrækkelig stor værdi og tilstrækkelig lav risiko (fx 150 og 0,75), så kan man komme ud for at skulle gøre indskud der overstiger risikofaktoren. I så fald bør man nok tjekke sin chancevurdering en ekstra gang. Som tidligere beskrevet er det dyrere at være for optimistisk, end det er at være for konservativ, så det er en god idé at overveje om man skal justere indskuddet ned for at være på den sikre side.
Personligt nedjusterer jeg indskuddet til risikofaktoren, medmindre jeg er helt sikker på at min chancevurdering er, måske ikke 100% korrekt, men meget tæt på. Derudover gør jeg aldrig indskud der er større end Kelly-strategien.
Test af de enkelte metoder
For at teste hvor effektive de enkelte metoder er, er her opsat følgende scenarie.
10.000 spil der har en tilfældigt og uniformt fordelt:
-
CV mellem 25% og 75%
-
BV mellem 101% og 107%
Følgende tre metoder er brugt til at bestemme indsatsstørrelsen (start balance = 100 units):

Risikofaktoren r=0,02 giver en gennemsnitlig indsats på 1,04%. For at udgangspunktet skal være det samme, er hhv. 1,04% og 1,04 units valgt til metode 2 og 1.
Efter at have simuleret ovenstående scenarie 1.000 gange, tegner der sig et billede af hvilken metode der giver det største afkast.
|
Andel af tests med størst afkast |
|
|
Metode 1 |
0,0% |
|
Metode 2 |
17,3% |
|
Metode 3 |
82,7% |
Metode 3 er langt overlegen. Desuden ser vi at flatbetting er og bliver noget man skal holde sig fra, hvis man vil optimere sit afkast. Metode 2 er metode 1 overlegen i mere end 95% af tilfældene.
Hvis Kelly-strategien var brugt, ville denne, ikke overraskende, være overlegen i 95,8% af tilfældene, men der er som tidligere nævnt en lang række grunde til ikke at følge den.
Hvad er en passende risikofaktor?
Hvis man kigger på det gennemsnitlige indskud, som Kelly-strategien gør i ovenstående scenarie, så er det på 4,2% af kapitalen. Med en risikofaktor på 0,08 får man et gennemsnitligt indskud i samme scenarie 4,16%. Det er meget aggressivt, og sikkert også for meget for de fleste.
De fleste vil nok have glæde af en risikofaktor på 0,02-0,05, men det er personligt og et spørgsmål om temperament. En ting man skal holde sig for øje er, at jo større risikofaktor, jo større vil udsvingene i kapitalen være.
Risikofaktoren kan blive for høj. At Kelly-strategien i snit spiller 4,2% af kapitalen, er en god indikation af at 0,08 er i en øvre ende af hvad det bør være. Hvis man eksempelvis havde en risikofaktor på 0,08, så ville spil 2 skulle have et indskud på 2,1%, hvor Kelly-strategien siger knap 1,6%. I sådanne tilfælde bør man altid, som minimum, nedjustere indsatsen til Kelly-bettet.
Den optimale risikofaktor
Der er naturligvis en sammenhæng imellem Kelly-strategien og denne metode. Ved at sætte en bestemt risikofaktor får man præcis Kelly-bettet:
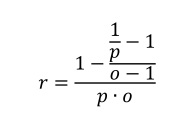
Som det ses er den optimale risikofaktor kun bestemt af chancevurderingen, p, og odds på spillet o.
Ved de tre spil vi tidligere har kigget på, ville man få følgende værdier for r:
Spil 1: 0,16
Spil 2: 0,06
Spil 3: 0,20
I det lys kan en anbefaling af at holde sin personlige risikofaktor nede under 0,05 måske virke for konservativt, men man skal huske grundene til at være mere konservativ end Kelly. Sæt ALDRIG mere end hvad Kelly-strategien siger.
Personligt benytter jeg 0,03 som risikofaktor i udgangspunktet, men det hænder at jeg for et enkelt spil justerer op eller ned. Op når jeg er meget sikker på at CV er korrekt og værdi er til stede, og ned når jeg er usikker på værdi og CV.
Det hører dog til sjældenhederne. Selvom der måske var mere at hente ved at justere oftere for hvert spil, så undlader jeg helst dette, simpelthen for at spare tid, men også fordi dette indsatsniveau rent mentalt passer mig ganske fint. Desuden ved jeg, at jeg allerede fanger det vigtigste, nemlig kontinuerlig justering for risiko og værdi.
Indskud på DNB: udregn chance
Der findes en lang række spil, fx visse asian handicaps, hvor man på et bestemt udfald får spillet annulleret. Når man her sætter sit indskud, bør man derfor justere for at spillet kan blive annulleret. Lad os sige at et spil har en CV på 45-20-35, hvor de 20% er på et udfald der udbetaler odds 1, altså pengene retur.
Her bør man se helt se bort fra no-bet udfaldet. Det efterlader os med en CV på 45-35. Dette summerer ikke til 100% og derfor er vi nødsaget til at justere chancevurderingen. Det kan vi gøre ved at tage sandsynligheden for udfaldet, og dele det med summen af alle udfald.
Sandsynligheden for at spillet går hjem bliver således 45/(45+35) = 56,25%. Når vi ser bort fra no-bet udfaldet, bliver den nye CV således 56,25%-43,75% (bemærk: bet valuen udregnes fortsat med den oprindelige CV, dvs inklusive chancen for no-bet-udfaldet).
Ved et spil med en 45-20-35 CV og odds 1,85 på de 45% med pengene retur 20% af gangene (dvs en bet value på: (45 x 1,85) + (20 x 1) = 103,25), vil indskuddet (med r = 0,02) altså blive:

Kvarte og halve asian-linjer
Derudover findes der forskellige Asian linjer. Hold kan både få halve og sågar kvarte handikap, men det er ikke synderligt kompliceret af den grund. Hvis linjen er halv (+0,5; +1,5; +2,5), så har spillet kun to udfald og man gør indskud som ved et hvert andet spil med to udfald.
Et spil på en kvart linje (+0,25; +0,75; +1,25) er reelt to spil. Et spil på +0,75 fremkommer ved at halvdelen af indskuddet spilles på +0,5 og den anden halvdel spilles på +1.
Lad as antage at ovenstående eksempel er en AH -1 linje, hvor der er 45% for sejr med to eller flere mål og 20% for sejr med præcis ét mål. AH -0,5 linjen svarer så til den rene sejr hvilket giver 65%. For at udregne indskuddet deler vi blot udregningen op i to.
For AH -1 spillet får vi således:
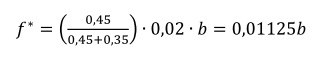
For AH -0,5 spillet får vi:
![]()
Da vi i princippet har lige meget på hver spil, vægter vi dem ens og det samlede indskud bliver på:
![]()
Lad os antage at bet valuen på netop dette spil er b=105% og vi får det samlede indskud til at være 1,27% .
For meget bøvl? Der er heldigvis en genvej, der er meget hurtigere og nemmere.
Den hurtige løsning
Selvom vi alle er interesserede i at optimere vores profit, så skal der også være en rimelig sammenhæng mellem den tid vi bruger på at finde indskudsstørrelsen, og det afkast vi får.
Der er formegentligt ingen, der har lyst til at bruge halve og hele timer på, at finde ud af, hvor mange penge man skal sætte. Derfor skal money management helst ikke udvikle sig til en halv matematiktest, hver gang man skal placere sit spil. Det skal være hurtigt og bekvemt.
Ovenstående metode er faktisk ikke så kompliceret, når man lige har vænnet sig til den, men man KAN skyde genvej.
En lynhurtig metode til at finde indskudsstørrelsen er:
![]()
Hvor f* er andelen af kapitalen der skal placeres på spillet;
p er sandsynligheden for at spillet går hjem (chancevurdering);
r er en risikofaktor med en værdi imellem 0 og 1 (ex: 0,02 betyder 2% af kapitalen)
Her får man ikke gjort et ekstra indskud for en høj værdi, til gengæld tager man højde for det absolut vigtigste, risikoen ved spillet. Metoden er naturligvis ikke så god som metode 3, men den er metode 1 og metode 2 langt overlegen. Hvis man samtidig har en fornuftig risikofaktor, så vil man stort set aldrig komme over Kelly-strategien og så sparer man den udregning.
En alternativ opskrivning er:
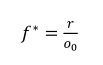
Hvis man ved, at et spil er spilbart ned til odds 1,50, er det nemt at finde indskudsstørrelsen til 1,33% (ved r=0,02). Dette gælder også for samtlige AH linjer og DNB spil! Ved at gange bet valuen på, får man præcis samme resultat som i forrige afsnit.
Flere spil på samme tid
En af forudsætningerne i Kelly, er at man kun har ét åbent bet af gangen. Det er i sagens natur ikke muligt hvis man eksempelvis gerne vil spille på to kampe der afvikles samtidigt, eller hvis man vil spille på ting som først afvikles engang ud i fremtiden. Personligt er det ikke noget jeg tager så tungt, men for fuldstændighedens skyld præsenteres problemstillingen nu alligevel.
Der er en fordel at få afgjort et spil, inden man sætter det næste. Såfremt man vinder, så kan indskud og gevinst geninvesteres med det samme. Man kan fristes til at tro at det er marginaler, men på den lange bane vil det betyde noget. Rentes rente sørger nemlig for en højere forrentning af kapitalen. Dette har vi allerede illustreret i eksemplet omkring udtrækning af kapital og fuld geninvestering.
Omvendt, hvis man taber spillet, så bliver man ikke ringere stillet, end hvis man satte det nye spil inden det første var afgjort. Dette ud fra en betragtning om at et indskud er ”tabt” indtil det modsatte er bevist. Hvis vi skal gå helt i detaljen, så burde åbne væddemål medregnes i kapitalen som indskud + forventet merværdi (indskud + bet value). I forlængelse af, at dette ikke skal blive for besværligt og tidskrævende, og taget i betragtning at vi foretrækker en konservativ tilgang, så ser vi dog bort fra dette.
Vores kapital er de penge vi har som ikke allerede er placeret på væddemål. Vi kommer som nævnt ud for at skulle have to sideløbende spil. Antag to kampe der har præcis samme sandsynlighed for en hjemmesejr (50%) og præcis samme odds for at det sker (2,10). Begge kampe har kick off på præcis samme tid.
Begge kampe skal have et indskud på 1,05% (r=0,02), men hvilken kamp skal vi spille på først? Med en startkapital på 100 sætter 1,05 units på den første kamp. Herefter er kapitalen 98,95 units så den næste kamp får kun 1,039 units. Man kan med rette argumentere for, at det er så små marginaler, at det ikke betyder det helt store. Hvis man gerne vil have et lige stort indskud kan det dog nemt udregnes.
Først finder man ud af hvor stor en andel man i alt skal sætte: 2,09 units
![]()
Disse skal så fordeles med halvdelen på hver.
Hvis det nu ikke var to ens kampe, lad os sige en kamp der skulle have 1% og en kamp der skulle have 2%, så skulle de fordeles med (1%/(1%+2%))=1/3 på den ene og (2%/(2%+1%))=2/3 på den anden.
Personligt er det ikke noget jeg bekymrer mig om. Jeg venter så vidt muligt med at sætte mine spil, indtil så mange af mine åbne som muligt er afgjort. Jeg kunne dog aldrig finde på at vente på en afgørelse, hvis jeg kan se, at et odds er på vej ned. Så højt odds som muligt har stadig topprioritet. Jeg justerer ikke for to sideløbende spil – det bliver til for meget arbejde i min verden.
Konklusion
Lad os slutteligt hurtigt opridse de vigtigste ting når det kommer til money management.
Betragt betting som en investering. Forsøg at få kapitalen til at yngle og lad være med at hæve af den i tide og utide.
Kelly-strategien er den optimale, men der er en del problemstillinger i forbindelse med at benytte den. Vi kan dog fra Kelly se, at risikoen ved spillet er vigtigere for indsatsen end værdien er. Samtidigt skal der dog også tages højde for værdi, således at større værdi bør have et større indskud.
Derudover er det vigtigt at justere sit indskud så ofte som muligt, helst efter hvert spil.
En metode, der tager højde for alle disse ting, er:
![]()
Den er langt overlegen i forhold til, at man spiller en fast procentdel, og ekstremt overlegen i forhold til, at man spiller et fast beløb.
Metoden indeholder en risikofaktor som man selv vælger. Denne bør ikke overstige 0,05 og må ikke overstige 0,8. Hvis man får et indskud, der er større end det som Kelly-strategien anbefaler, så bør man under alle omstændigheder nedjustere til Kelly-bettet.
Når man spiller på kampe hvor et udfald udbetaler odds 1, bør man justere sandsynligheden for at spillet går hjem derefter. Det samme gælder for diverse halve og kvarte asiatiske linjer.
Et hurtigere alternativ kunne være:
![]()
Eller
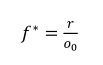
Metoden tager ikke højde for, at større værdi bør have et større indskud, men er stadig flatbetting og betting med en fast procentdel langt overlegne.
Forsøg så vidt muligt at få afgjort satte spil inden et nyt sættes, det giver større profit i sidste ende, men gør det ikke på bekostning af et højere odds!
Kilder
-
Kelly, J. L., Jr. (1956), "A New Interpretation of Information Rate", Bell System Technical Journal 35: 917–926
-
Poundstone, William (2005), “Fortune's Formula: The Untold Story of the Scientific Betting System That Beat the Casinos and Wall Street”, New York: Hill and Wang
-
Thorp, E. O. (January 1961), "Fortune's Formula: The Game of Blackjack", American Mathematical Society
-
Thorp, E.O. (June 1997), “The Kelly Criterion in Blackjack, Sports Betting, and the Stock Market”, The 10th International Conference on Gambling and Risk Taking
-
Thorp, E. O. (May 2008), "The Kelly Criterion: Part I", Wilmott Magazine











